Apa itu gelombang stasioner? apa saja jenis gelombang stasioner? bagaimana rumus dan contoh soal gelombang stasioner? Untuk mengetahui lebih lengkap tentang gelombang stasioner, berikut ini kami jelaskan secara lengkap tentang pengertian gelombang stasioner, jenis gelombang stasioner, rumus dan contoh soal gelombang stasioner dengan penjelasan terlengkap.
Pengertian Gelombang Stasioner
Gelombang stasioner merupakan gabungan dari dua gelombang yang memiliki frekuensi, cepat rambat dan amplitudo sama besar tapi merambat pada arah berlawanan.
Jadi, gelombang stasioner adalah perpaduan atau super posisi dari dua gelombang yang identik tapi berlawanan arah.
Contoh gelombang stasioner pada gelombang tali yang diikat di salah satu ujungnya, dan ujung lainnya di ayunkan naik turun. Proses tersebut menimbulkan gelombang dating dan setelah menumbuk tiang akan mengalami gelombang pantul. Ketika gelombang datang dan gelombang pantul bertemu dan berpadu, maka fenomena gelombang stasioner bekerja.
Nilai maksimum dan nilai minimum besar amplitudo gelombang stasioner berubah-ubah. Titik aplitudo nilai maksimum disebut dengan perut dan titik aplitudo nilai minimum disebut dengan simpul.
Baca Juga : Pengertian Fluks Magnetik dan Penjelasannya
Jenis Gelombang Stasioner
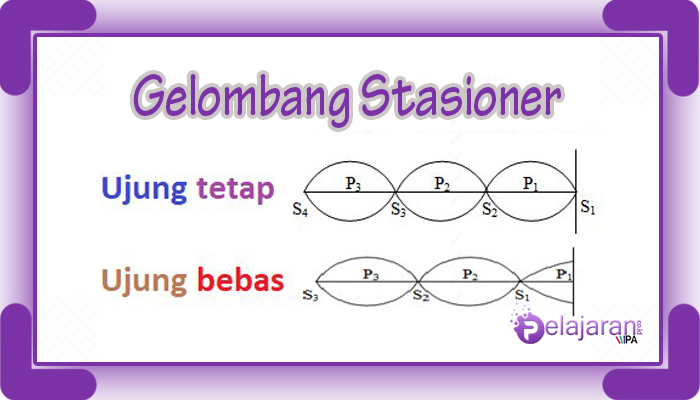
Gelombang stasioner dibagi menjadi dua jenis, yaitu gelombang stasioner pada ujung tetap dan gelombang stasioner ujung bebas. Berikut penjelasannya:
Gelombang Stasioner Pada Ujung Tetap
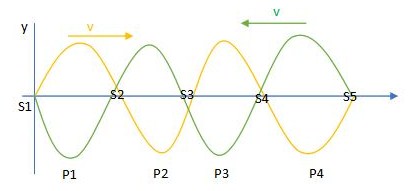
Perhatikan gambar dibawah ini:
Berdasarkan gambar tersebut, diketahui pada ujung tetap (terikat) akan membentuk 2 gelombang tali dengan arah berlawanan. Masing-masing memiliki persamaan gelombang seperti berikut:
y1 = A sin (ωt – kx) (merambat ke arah kanan)
y2 = A sin (ωt + kx) (merambat ke arah kiri)
Super posisi dari kedua gelombang itu dinyatakan :
ys = y1 + y2 = 2A sin kx cos ωt
Amplitudo gabungan Ap sebesar Ap = 2A sin kx
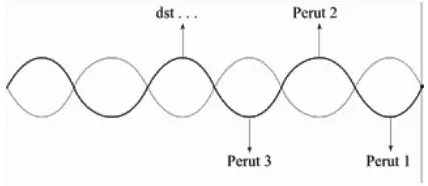
Menentukan Simpul Dan Perut
Simpul pertama yaitu titik awal berarti jarak dari titik pantul = 0. Simpul kedua merupakan ½ λ, simpul ketiga yaitu λ, keempat 1 ½ λ dst.
Perut pertama merupakan ¼ λ, perut kedua ¾ λ, perut ketiga 1¼ λ dst.
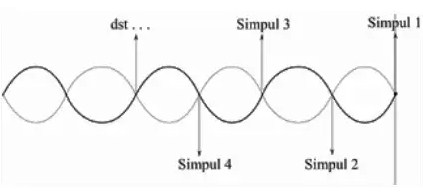
Cara Menentukan simpul gelombang pada ujung terikat
Perhatikan gambar dibawah ini:
Dari gambar tersebut tertera nama-nama simpul gelombang. Untuk menentukan letak-letak dari simpul tersebut dapat menggunakan persamaan berikut ini:
xn+1 = (2n) λ /4
n = 0, 1, 2, . . .
Untuk simpul ke-1, n = 0, perut ke-2, n = 1 dan seterusnya.
Baca Juga : Pengertian Gaya Normal dan Penjelasannya
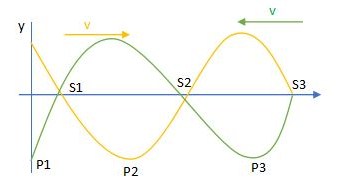
Gelombang Stasioner Pada Ujung Bebas
Perhatikan gambar dibawah ini:
Berbeda dengan ujung terikat, ujung bebas memiliki persamaan seperti dibawah ini:
ys = y1 + y2 = 2A cos kx sin ωt
Amplitudo gabungan (Ap)
sebesar Ap = 2A cos kx.
Menentukan Simpul Dan Perut
Simpul pertama yaitu ¼ λ, simpul kedua = ¾ λ, dan simpul ketiga = 1¼ λ dst.
Perut pertama adalah titik awal berarti jarak dari titik pantul = 0. perut kedua yaitu ½ λ, perut ketiga merupakan λ, keempat 1 ½ λ dst.
Menentukan Persamaan Gelombang
Pada umunya persamaan gelombang stasioner dapat dituliskan sebagai berikut:
y = 2A sin kx cos ωt
y = Ap sin cos ωt
dengan Amplitudo Stasionernya: 2A sin kx
Keterangan:
Ap adalah Amplitudo Gelombang Stasioner (m)
k adalah Bilangan Gelombang
λ adalah Panjang Gelombang (m)
Cara Menentukan Letak Simpul Pada Ujung Bebas Gelombang Stasioner
Perhatikan gambar dibawah ini
Berdasarkan gambar tersebut, dapat dilihat nama-nama perut gelombang. Untuk mengetahui letak gelombang yang dihitung dari ujung gelombang dapat menggunakan persamaan seperti berikut:
xn+1 = (2n + 1) λ/4
n = 0, 1, 2, . . .
Untuk simpul ke-1, n = 0, perut ke-2, n = 1 dan seterusnya.
Baca Juga: Gelombang Cahaya dan Penjelasannya.
Rumus Gelombang Stasioner
Terdapat beberapa rumus yang digunakan dalam persamaan gelombang mekanik, diantaranya seperti berikut ini:
Persamaan gelombang stationer ujung terikat
y1 = A sin (ωt-kx)
y2 = A sin (ωt+kx)
Jika persamaan gelombang adalah negative, maka gelombang berjalan ke kanan. Sedangkan jika gelombang bertanda positif, maka gelombang berjalan ke kiri.
Super posisi kedua gelombang
ys = y1 +y2 = 2A sin kx cos ωt
Keterangan:
y1 dan y2 = persamaan gelombang (m)
A = Amplitudo (m)
ω = kecepatan sudut
t = waktu (s)
x = posisi (m)
ys = super posisi gelombang (m)
Baca Juga : Gelombang Bunyi dan Penjelasannya
Contoh Soal Gelombang Mekanik
Diketahui sebuah tali memiliki panjang 10 meter, salah satu ujung tali terikat pada sebuah pohon dan ujung satunya digerakkan secara kontinu dengan amplitudo 10 cm serta frekuensi 5 Hz. Jika cepat rambat tali tersebut sebesar 5 m/s. Berapakah aplitudo pada titik P yang terletak pada jarak 2m dari ujung terikat tali tersebut.
Pembahasan
Diketahui
Panjang tali (l) = 10m
Ujung terikat
A = 10 cm
f = 5Hz
v = 5 m/s
Penyelesaian
v = λf
5 = λ 5
λ = 1m
Ap = 2A sin kx
Ap = 2 A sin 2 pi x/ λ
Ap = 2 10 sin 2 pi 2 / λ
Ap = 2 10 0
Ap = 0 m
Jadi amplitude pada jarak 2 m di titik P adalah 0 m. Keadaan itu berarti amplitude pada keadaan simpul gelombang yang menjadikan nilai amplitude di titik P bernilai 0.
Baca Juga : Gelombang Mekanik dan Penjelasannya
Demikian artikel mengenai Gelombang Stasioner dan Penjelasannya. Semoga artikel ini dapat bermanfaat dan menambah wawasan anda mengenai pelajaran Ilmu Pengetahuan Alam.