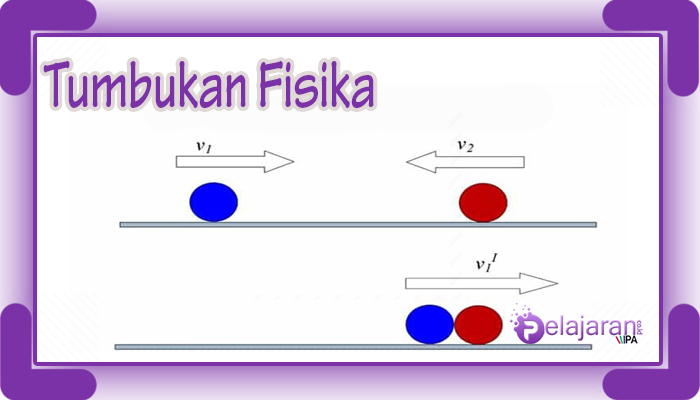
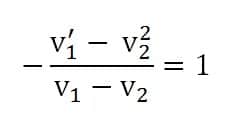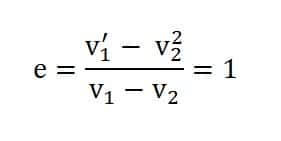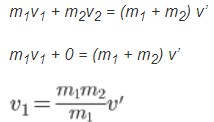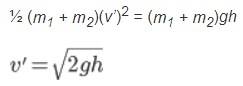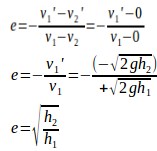Secara teori, tumbukan atau lentingan juga disebut sebagai pantulan. Hal ini karena sebuah benda yang bergerak mengenai benda lain yang diam atau bergerak. Hasil dari masing-masing tumbukan memiliki dua karakter yang berbeda, ada yang sempurna dan tidak sempurna, ada pula yang sebagian.
Berdasarkan sifat kelentingan benda bertumbukan, tumbukan dibagi menjadi tiga jenis, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian dan tumbukan tidak lenting sempurna. Untuk lebih jelasnya dibawah ini akan dijelaskan secara lengkap tentang tumbukan dan jenis-jenis tumbukan.
Baca Juga : Pengertian Usaha dan Energi dan Penjelasannya
Tumbukan Lenting Sempurna
Tumbukan lenting sempurna terjadi ketika momentum dan energi kinetik masing-masing benda sebelum tumbukan SAMA dengan momentum dan energi kinetik masing-masing benda setelah tumbukan. Penggunaan kata lenting pada jenis tumbukan ini mengartikan pada setelah terjadi tumbukan, kedua benta tidak bergabing menjadi satu atau tidak saling menempel melainkan memantul.
Dengan demikian, pada tumbukan lenting sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik.
Baca Juga : Tumbukan Lenting Sempurna
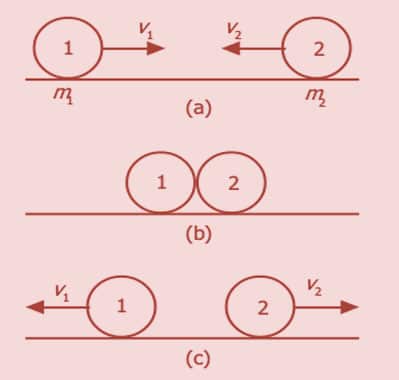
Hukum Kekekalan Momentum dapat digambarkan sebagai berikut: terdapat dua buah benda dengan masing-masing masa m1 dan m2 bergerak dengan kecepatan v1 dan v2 dengan arah berlawanan, perhatikan gambar dibawah ini.
Keterangan :
a. sebelum tumbukan
b. saat tumbukan
c. setelah tumbukan.
Ketika kedua benda saling bertumbukan lenting sempurna, maka setelah terjadi tumbukan kecepatan kedua benda menjadi v1′ dan v2′ . Berdasarkan Hukum Kekekalan Momentum, maka dituliskan:
m1 v1 + m2 v2 = m1 v1‘ + m2 v2‘
m1 v1 – m1 v1‘ = m2 v2‘ – m2 v2
m1 (v1 – v1‘ ) = m2 (v2‘ – v2)
(persamaan i)
Diperoleh Hukum Kekekalan Energi Kinetik :
1/2m1v12 + ½ m2v22 = ½ m1(v1’)2 + ½ m2(v2’)2
m1v12 + m2v22 + m2v22 = m1(v1’)2 + m2(v2’)2
m1(v12 – (v1’)2) = m2((v2’)2 – v22)
m1(v1 + v1’)(v1 – v1’) = m2 (v2’ + v2) (v2’-v2)
(persamaan ii)
Jika persamaan (i) dibagi dengan persamaan (ii), maka diperoleh persamaan sebagai berikut:
v1 + v1‘ = v2‘ + v2
v1‘ – v2‘ = v2 – v1
v1‘ – v2‘ = -(v1 – v2)
(persamaan 2)
persamaan (2) dapat dituliskann sebagai berikut:
(Persamaan 3)
Bilangan persamaan (3) disebut dengan koefisien restitusi (e) yang merupakan kecepatan perbandingan kecepatan relatif kedua benda sebelum tumbuhan, persamaan (3) dapat dinyatakan sebagai berikut:
Dengan demikian, pada tumbukan lenting sempurna koefisien restitusi (e) = 1.
Baca Juga : Pengertian Suhu, Rumus dan Penjelasannya
Tumbukan Tidak Lenting Sempurna
Pada tumbukan tidak lenting sempurna, kecepatan benda-benda setelah tumbukan sama besar (benda yang bertumbukan saling melekat). Contohnya, tumbukan antara peluru dengan sebuah target dimana setelah tumbukan peluru mengerem dalam target. Secara matematis, tumbukan tidak lenting sempurna dirumuskan sebagai berikut:
m1v1 + m2v2 = m1v’1 + m2v’2
Jika v’1 = v’2 = v’, maka m1v1 + m2v2 = (m1 + m2) v’
Tumbukan tidak lenting sempurna yang terjadi antara dua benda
Contoh tumbukan tidak lenting sempurna seperti ayunan balistik. Ayunan balistik adalah seperangkat alat yang digunakan untuk mengukur benda yang bergerak dengan kecepatan cukup besar, misalnya kecepatan peluru. Prinsip kerja ayunan balistik berdasarkan hal-hal berikut, yaitu:
Penerapan sifat tumbukan tidak lenting sempurna
Hukum kekelan energi mekanik
Ketika persamaan pertama di subtitusikan ke persamaan kedua, maka diketahui kecepatan peluru sebelum bersarang dalam balok.
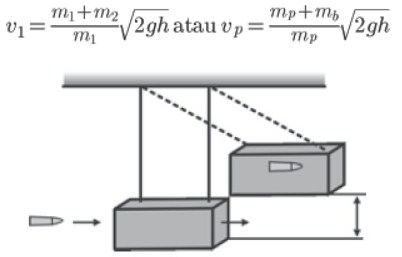
Skema ayunan balistik
Baca Juga : Pengertian Jangka Sorong dan Penjelasannya
Tumbukan Lenting Sebagian
Pada tumbukan lenting sebagian, ada beberapa energi kinetik yang diubah menjadi energi dalam bentuk lain, seperti energi panas, bunyi dan sebagian. Hal ini menyebabkan energi kinetik sebelum tumbukan lebih besar dibandingkan energi kinetik sesudah tumbukan. Sebagian besar tumbukan yang terjadi antara dua benda merupakan tumbukan lenting sebagian.
Pada tumbukan lenting sebagian berlaku hukum kekebalan momentum, namun tidak berlaku HUkum Kekebalan Energi Kinetik.
ΣEk > ΣEk ‘ , maka:
Ek1 + Ek2 > Ek1′ + Ek2′
v2 – v1 > v1′ – v2’
Sehingga persamaan (3) dapat dituliskan:
Dengan demikian, dapat disimpulkan pada tumbukan lenting sebagian, koefisien restitusi (e) adalah: 0 < e < 1.
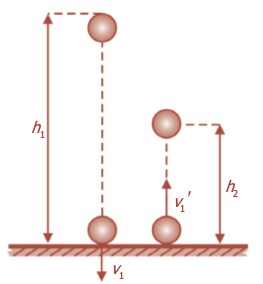
Untuk menentukan koefisien restitusi benda yang bertumbukan, perhatikan contoh berikut ini. Perhatikan gambar berikut!
Sebuah bola elastis jatuh bebas dari ketinggian h1 dari lantai, maka akan terjadi tumbukan antara bola dengan lantai sehingga bola memantul setinggi h2. Berdasarkan persamaan pada gerak jatuh bebas, kecepatan benda sesaat sebelum tumbukan adalah:
Gerak bola sesaat setelah terjadi tumbukan dapat diidentifikasikan dengan gerak jatuh bebas, sehingga:
Karena lantai diam, maka kecepatan lantai sebelum dan sesudah tumbukan adalah nol, v2 = v2 ‘ = 0, sehingga besarnya koefisien restitusi adalah:
Baca Juga : Momentum & Impuls dengan Penjelasannya
Demikian artikel mengenai Tumbukan Fisika Penjelasannya. Semoga artikel ini dapat bermanfaat dan menambah wawasan anda mengenai pelajaran Ilmu Pengetahuan Alam.