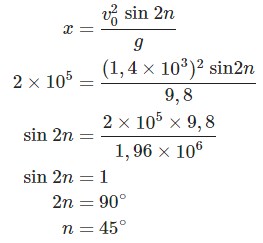Gerak parabola adalah gerak antara dua dimensi benda yang bergerak membentuk sudut elevasi dengan sumbu x atau sumbu y. Salah satu contoh derak parabola yaitu pada bola yang dilempar maka akan mencapai ketinggain tertentu sebelum kembali turun tertarik gravitasi. Gerak pada bola inilah yang disebut dengan gerak parabola. Lalu apa itu gerak parabola sebenarnya?
Untuk mengetahui lengkap tentang gerak parabola. Berikut ini akan dijelaskan secara lengkap tentang pengertian gerak parabola, rumus gerak parabola dan contoh soal gerak parabola dengan pembahasannya.
Baca Juga : Gelombang Transversal dan Longitudinal dengan Penjelasannya
Pengertian Gerak Parabola
Gerak parabola disebut juga gerak peluru yang memiliki bentuk lintasan parabola. Gerak parabola merupakan gabungan dari gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB).
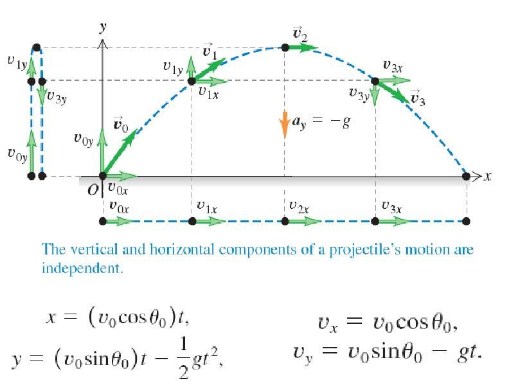
Gerak parabola adalah gerak dua dimensi benda yang bergerak membentuk sudut elevasi dengan sumbu x atau sumbu y. Sumbu x (horizontal) adalah GLB dan sumbu y (vertikal) adalah GLBB. Kedua gerak tersebut tidak saling mempengaruhi namun membentuk suatu gerak parabola. Saat terjadi gerak parabola, diasumsikan tidak ada hambatan dari udara sehingga benda jatuh dengan percepatan yang sama.
Untuk lebih jelasnya, perhatikan contoh gerak parabola berikut ini. Sebuah bola dilemparkan dari sebuah gedung dengan kecepatan awal horizontal sebesar Ux dan kecepatan awal vertikalnya Uy = 0. Komponen kecepatan dalam horizontal adalah konstan atau tetap, hal ini karena tidak ada percepatan dalam arah horizontal. Sedangkan kecepatan vertikal mengalami percepatan yang sama dengan percepatan gravitasi (9,8 ms-2).
Berapa lamanya bola di udara tergantung dari gerak vertikalnya, sedangkan besar dan arah kecepatan bola seiring waktu akan terus berubah.
Besar kecepatan bola dapat dirumuskan sebagai berikut:
V = √Vx² + Vy²
vy = komponen kecepatan bola dalam arah vertikal
vx = komponen kecepatan dalam arah horizontal (konstan)
Arah kecepatan benda pada gerak parabola dapat ditentukan dengan rumusan sebagai berikut:
tan θ = vy / vx
Baca Juga : Kelajuan, Kecepatan, dan Percepatan dengan penjelasannya
Komponen Gerak Parabola
Perhatikan pada gambar ilustrasi dibawah ini..
Gerak Parabola merupakan gabungan dari dua komponen gerak, yaitu komponen gerak horizontal (sumbu x) dan komponen gerak vertikal (sumbu y). Berikut penjelasannya..
Komponen Sumbu x
Komponen sumbu x merupakan komponen GLB. GLB adalah kecepatan sumbu horizontal pada titik atau posisi tetap. Di sumbu x komponen awal adalah simbol dari kecepatan awal.
Secara matematis, rumus yang berlaku adalah sebagai berikut:
Vox = Vo cos θ
Keterangan:
Vox = kecepatan awal di sumbu x (m/s)
Vo = kecepatan awal (m/s)
θ = sudut elevasi
Komponen Sumbu y
Komponen sumbu y merupakan komponen GLBB. GLBB adalah sebuah simbol perpindahan atau jarak pada sumbu x ditunjukkan dengan s, sedangkan sumbu y di tunjukkan dengan y.
Secara matematis, rumus yang berlaku pada sumbu y adalah sebagai berikut:
Voy = Vo sin θ
Keterangan:
Vox = kecepatan awal di sumbu y (m/s)
Vo = kecepatan awal (m/s)
θ = sudut elevasi (o)
Contoh gerak parabola dalam kehidupan sehari-hari, seperti:
- Shooting yang dilakukan oleh pemain basket
- Menerbangkan pesawat kertas
- Menendang bola yang semula diam dengan punggung kaki
- Melesatkan batu yang dipasang pada ketapel
Baca Juga : Percepatan Gravitasi dan Penjelasannya
Rumus Gerak Parabola
Gerak parabola memiliki dua komponen, yaitu sumbu x dan sumbu y, rumus yang berlaku pada kedua komponen tersebut adalah:
Rumus gerak parabola sumbu x, yaitu
vx = v0x = v0 cos α
x = vxt = v0 cos α t
Keterangan:
vx = kecepatan akhir benda pada sumbu x (m/s) ;
v0 = kecepatan awal benda (m/s)
α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
t = waktu yang dibutuhkan untuk menempuh lintasan parabola
Rumus gerak parabola sumbu y, yaitu:
Gerak secara vertikal akan dipengaruhi oleh gaya gravitasi
vy = v0y – gt
Sedangkan pada sumbu vertikal v0y = v0 sin α, maka
vy = v0 sin α – gt
Pada penguraian gerak parabola pada sumbu y, maka diketahui posisi benda sebagai berikut:
y = v0y t – ½ gt2
atau
y = v0 sin α t – ½ gt2
Keterangan:
vy = kecepatan akhir benda pada sumbu y (m/s) ;
v0y = kecepatan awal benda (m/s)
α = sudut elevasi yang terbentu antara sumbu x dengan lintasan
t = waktu yang dibutuhkan untuk menempuh lintasan parabola
Berikut ini beberapa persamaan matetamtis yang berlaku pada gerak parabola, antara lain:
Kecepatan benda pada gerak parabola yang diuraikan pada komponen sumbu x dan sumbu y secara matematis di rumuskan sebagai berikut:
Arah benda gerak parabola pada komponen sumbu x secara matematis dirumuskan sebagai berikut:
tan θ = vy / vx
Sehingga nilai vx selalu positif namun tergantung pada nilai vy
Pada komponen sumbu y benda akan memiliki kecepatan sama dengan nol, ketika benda berada pada tinggi maksimum, maka secara matematis rumus yang dituliskan adalah sebagai berikut:
tAB = (v0 sinα)/ g
Rumus tinggi maksimum benda pada komponen sumbu x yaitu:
H =( v02 sin2α)/2g
Jarak tempuh maksimum benda pada komponen sumbu x yaitu:
X =v0xtAC = v0cosα 2(v0 sinα/g) = v022 (sinα/g) cos α
X =( v02 sin 2α)/g
Baca Juga : Gerak Jatuh Bebas dan Penjelasannya
Contoh Soal Gerak Parabola
Soal 1.
Peluru ditembakkan condong ke atas dengan kecepatan awal v=1,4×10−3 m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2×105 m. Bila percepatan gravitasi 9,8 m/s2, maka elevasinya adalah n derajat, dengan n sebesar…
Penyelesaian:
Jarak horizontal terjauh untuk contoh soal gerak parabola adalah
Soal 2:
Sebuah bola ditendang dengan kecepatan awal bola tersebut 20 m/s, sudut elevasi yang terbentuk antara lintasan bola dengan sumbu x yakni 370 (sin 370 = 0,6). Dan percepatan gravitasinya sebesar 10 m/s2, hitunglah tinggi maksimum dan jarak maksimum yang dapat dicapai oleh bola tersebut
Pembahasan
Diketahui
v0 = 20 m/s ; α = 370
Penyelesaian:
H =( v02 sin2α)/2g
H = (202 sin 2 370)/2.10
H = (202 (0,6) 2)/2.10
H = 7,2 m
X = ( v02 sin 2α)/g
X = (202 2(sin 370 cos 370))/10
X = 38,4 m
Maka, tinggi maksimum yang dapat dicapai oleh bola yaitu 7,2m dan jarak terjauh yang dapat dicapai bola yaitu 38,4 m.
Baca Juga : Gerak Melingkar Beraturan
Demikian artikel mengenai Gerak Parabola dan Penjelasannya. Semoga artikel ini dapat bermanfaat dan menambah wawasan anda mengenai pelajaran Ilmu Pengetahuan Alam.